Sorting and Searching

SORTING

is needed to speed up searching operation.

There are 2 types of sorting based on the final condition of the data: Ascending and Descending.

Sorting also can be divided into 2 types of sort based on their difficulties.
1. Simple Sort : Bubble Sort, Selection Sort, and Insertion Sort.
2. Intermediate Sort : Quick Sort and Merge Sort.


Here I'm going to explain a little bit about my understanding in types of Sorting:

1. Bubble sort : compares 2 variables that are next to each other, swap if certain condition are met, until the end if the data.




2. Selection sort : compares 2 variables, starts from the first element to the second. After that, it compares the first element to the third, and so on. If certain condition are met, it will do a swap between the variables.




3. Insertion sort : has the same principle as having a temporary container to store certain data that is going to be swapped.



4. Quick Sort : it has a kind of 'recursive' scheme to execute this sorting type.



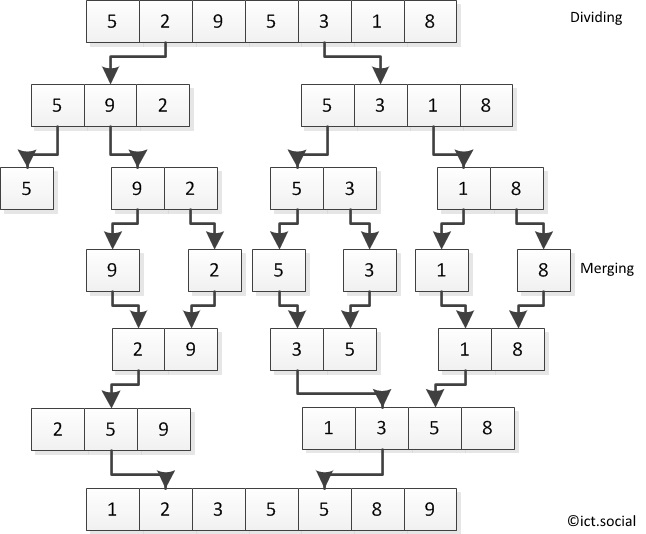
5. Merge Sort : based on 'divide-and-conquer" algorithm. Divide means we divide the data into 2 groups, then we solve each of the problems in the subsets, and lastly, we combine both solutions from each subsets, into one final solution.

SEARCHING

is needed to find certain data or element that is stored in a large array, and then to retrieve the data itself. We need to determine the key value to simplify the searching activity through our data. KEY must be unique for each data in a particular data lists or array.
For example, every employer have their own ID number, name, gender, address, date of birth, etc. But the unique value from each of them that is different from the other is their ID number. Thus, ID number can be used as a key when we do searching there.

There are some types of searching:
1. Linear search : compares each element of the array to the key.




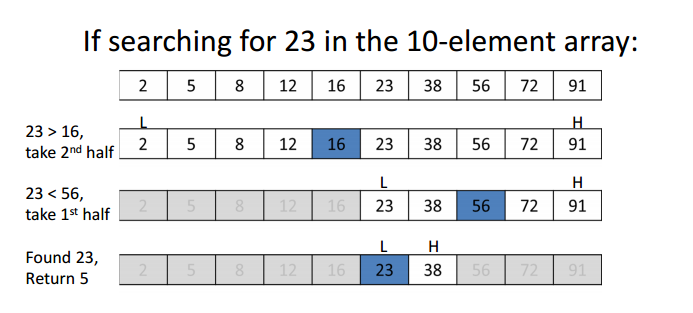
2. Binary search : we divide the data into 2 groups from the middle.



3. Interpolation search : split and look for approximate location of the data.
    The formula is :
                          key - data[min]
          Mid = ---------------------------  x (max-min) + min
                     data[max] - data[min]
 

Struct and File

On 5th December 2018, we continued to learn Algorithm and Programming course. We got informations about Structure and Files.

STRUCT

Structure is a data type to store various kind of variable's data types.
syntax:
struct name_of_structure{
      dataType1 name1;
      dataType2 name2;
     ...
};

Typedef is an alias to simplify the naming of structures.
example :
typedef struct BINUSIAN{
     int ID;
     int age;
     char name[101];
     ...
}mhs;

FILE

Data File is a place to save data from keyboard. While stream is all input and output data.
There are 3 standard streams activated when opening C program:
1. Standard Input stream
2. Standard Output stream
3. Standard Error stream

We can define File into 2 definition : Text file and Binary file.
Text File saved in text format / ASCII File.
Binary File saved in affixed format in line with micro-processor format.

The syntax:
FILE *variable_of_file;
     var_of_file = fopen ("Location of file\\filename.txt","w");

fclose (var_of_file);

There are many file modes (as I stated before as an example, with 'w' alphabet)
w: write or create a new file.
r: read a file.
a: append, to add data into the file.
rb: read binary file.
wb: write binary file.

How to "write" new data into the File? use fprintf, fputs, fputc
How to "read" an existing file? use fscanf, etc.

Usually, we are able to use IF condition, to check whether the file exist or no. Syntax:
if (var_of_file !=NULL){
     statements;
} else {
     printf ("File does not exist!\n");
}

Data file

asdasd

Function and Recursion

On the same day with the Cloud Computing Seminar in the Auditorium of BINUS Anggrek, we learned about function and recursion.

FUNCTION

Are also called : Sub-program, where we group some statements to do a particular job.
There are some advantages of using modular programming or using function:
1. Can be done by more than one programmer
2. Easier to debug and modification will not affect the whole program.
3. Easier to be documented.

the syntax of function is:
return-value-type function_name(parameter_lists){
     statements;
}

There are 2 types of function, one that returns value to the main function, and the other one who doesn't, called void function.

There are 2 ways to pass a parameter/parameters:
1. By Value : we pass the value of the variables.
2. By Reference : we are using pointer, to point at certain variables that we need.

RECURSION

Recursion function is a function that calls itself.
In recursion we have to define 2 things: Base case and the Reduction steps. Base case shows the simplest function that has to be done.

There are some case examples that use Recursion, for example to accumulate certain numbers, Fibonacci sequences, finding binary numbers, etc.

CLOUD COMPUTING - Seminar

On 28th November 2018, i attended a seminar through Algorithm and Programming learning session. The topic was about Cloud Computing.

Cloud refers to a Network or internet which is present at certain place, and accessible from any network.

Then about the Cloud Computing itself, it means to manage, accessing, and configuring data online, which are delivered as a network services.

Cloud Computing tends to separate infrastructure with business. The term 'Infrastructure' refers to hardware, networking, and software, as an entity. While 'Business' refers to procedural methods or workflow and strategic environment.

There are 3 kinds of Cloud Service models:

1. Cloud Software as a Service (SaaS) :offers application through a web browser.

2. Cloud Infrastructure as a Service (IaaS) : provides the hardware and the OS to the customers.

3. Cloud Platform as a Service (PaaS) : provides networked computers in a hosted environment with supports for its development.

Pointer and Array

Today, on Wednesday, 17th October 2018, we had lecture again in the auditorium at BINUS Anggrek.

Today's quizzes also require knowledge about pointer and arrays.

 Pointer 

Pointer is a variable that store the address of another variable.

syntax: *ptr_name(same as assigning variable);

For example:

int a=5;

int *ptr_a;

ptr_a=&a; //ptr_a refers to the address of a.

*ptr_a=10;

printf ("%d", a);

so the output will be  10, because we assigned a new value of ptr_a which is 10, and this also affect the value of a.

 Arrays 

Array is a structure data that gathers the same type of many data using the same name

syntax: [dimensional_value]   (identifier as the name of the array.)

To initialize:

     int numbers[10] //array will provide 10 spaces, with the index starts from 0 to 9.

Another way to initialize an array without declaring the dimensional value:

     int number[]={2,4,5,3,1,...}

If you want to assign a value to certain indexes of array, you can do:

     A[5]=10; //the fifth 'box' of the array will be filled with 10.

To access an element in the array, you can do:

     printf ("%d",A[5]); or printf ("%d", *(A+5)); //accessing the second 'box' of the array

Array can be multidimensional. For example:

2D : type identifier[...][...] //first dimension refers to rows, second dimension refers to columns